❓ 문제
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
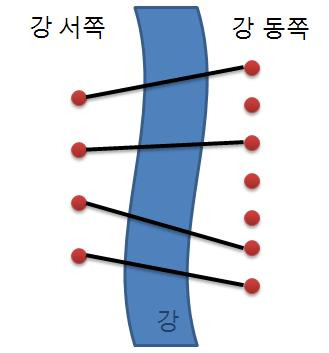
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.
📥 입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
📤 출력
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.
📥 예제 입력
3
2 2
1 5
13 29
📤 예제 출력
1
5
67863915
👩🏻💻 내 코드
import java.util.Scanner;
public class 다리놓기{
// 조합 계산
public static long combination(int m, int n) {
// 예: C(m, n) = m * (m - 1) * ... * (m - n + 1) / (n * (n - 1) * ... * 1)
long result = 1;
for (int i = 1; i <= n; i++) {
result = result * (m - i + 1) / i;
}
return result;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int T = in.nextInt();
for (int i = 0; i < T; i++) {
int N = in.nextInt();
int M = in.nextInt();
System.out.println(combination(M, N));
}
}
}
💡 코드 접근
- 강을 건너는 다리를 최대한 많이 짓는 경우의 수를 구하는 문제
- 서쪽의 사이트 N개에서 동쪽의 사이트 M개 중 N개의 사이트를 선택하여 다리를 지을 수 있다.
- 이는 "M개 중 N개를 선택하는 조합"을 계산하는 문제로, 조합의 기본 공식을 사용해야한다!!
- 조합 공식

저번 문제와 같이 팩토리얼 계산에서 값이 매우 커질 수 있기 때문에 int 대신 long 자료형 사용하는 게 적합하다
- 전체 팩토리얼을 계산하는 대신, 조합 계산에서 중간 나눗셈을 통해 작은 값들만 다루도록 최적화 할 수 있ㄷ.
- EX ) C(M,N)은 큰 수의 곱셈을 피하기 위해 m×(m−1)×⋯×(m−n+1)을 계산하고, 그 과정에서 각 값을 나누어 N!의 효과를 얻는 방식으로 최적화
- 조합 계산 공식

💡 알게 된 점
- 조합 계산 최적화는 큰 수의 팩토리얼을 모두 계산하는 방식보다 훨씬 효율적 >> 중간에 발생하는 나눗셈을 통해 큰 값들을 줄여가며 계산하는 방법이 유리합니다.
- 자료형: 계산 도중 값이 클 수 있으므로 문제의 조건에 맞게 적절한 자료형(예: long)을 선택하는 것이 중요
반응형
'백준 문제 풀이' 카테고리의 다른 글
| <코테 챌린지> 죽음의 게임 (백준 17204번) (4) | 2024.10.20 |
|---|---|
| <코테 챌린지> 순열 사이클 (백준 10451번) (0) | 2024.10.19 |
| <코테 챌린지> 부녀회장이 될테야 (백준 2775번) (1) | 2024.10.16 |
| <코테 챌린지> 피보나치 수 2 (백준 2748번) (0) | 2024.10.15 |
| <코테 챌린지> 빙고 (백준 2578번) (1) | 2024.10.14 |
