설명
아래 그림과 같은 이진트리를 레벨탐색 연습하세요.
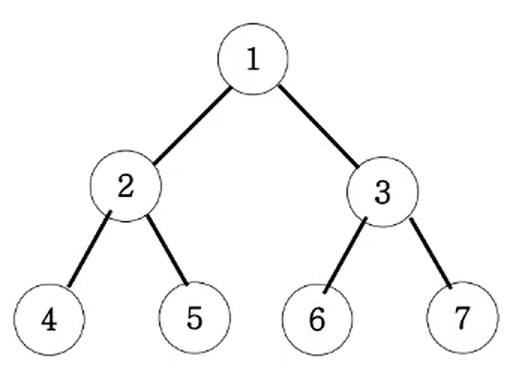
레벨 탐색 순회 출력 : 1 2 3 4 5 6 7
문제 해결
레벨 탐색은 말 그대로 레벨 별로 탐색하는 것이다.
루트에서 한 번만에 갈 수 있는 애들을 모두 방문하고, 두 번만에 갈 수 있는 애들을 방문하고 ... 이런 식의 과정이다.
BFS의 핵심은 큐를 이용하는 것이다. (Queue => FIFO 구조)
이전에 이진트리를 구성했던 방법대로 위 문제 사진과 같이 이진트리를 만들어준다
static Node root;
public static void main(String[] args) {
root = new Node(1);
root.lt = new Node(2);
root.rt = new Node(3);
root.lt.lt = new Node(4);
root.lt.rt = new Node(5);
root.rt.lt = new Node(6);
root.rt.rt = new Node(7);
BFS(root);
}
while (!queue.isEmpty()){
int len = queue.size();
System.out.print(L + " : ");
for (int i = 0; i < len; i++) {
Node currentNode = queue.poll(); // 큐에서 하나 꺼내고 출력
System.out.print(currentNode.data + " ");
if(currentNode.lt!=null) queue.offer(currentNode.lt);
if(currentNode.rt!=null) queue.offer(currentNode.rt);
}
L++;
System.out.println();
}- 각 반복마다 현재 큐의 크기(len)를 확인하는데, 이 때의 크기는 현재 레벨에 있는 노드의 수를 의미한다.
- 해당 레벨의 모든 노드를 큐에서 하나씩 꺼내고 그 값을 출력하고, 해당 노드의 자식이 있으면 그 자식들을 큐에 추가하는 방식이다. 이 과정을 반복해주면 된다.
- 레벨이 하나 완료되면 레벨 카운터(L)를 증가시킨다.
- 큐가 비어있지 않는 동안 위 과정을 반복해주면 된다.!!
최종 코드
import java.util.LinkedList;
import java.util.Queue;
public class P07_이진트리레벨탐색_BFS {
static Node root;
public static void main(String[] args) {
root = new Node(1);
root.lt = new Node(2);
root.rt = new Node(3);
root.lt.lt = new Node(4);
root.lt.rt = new Node(5);
root.rt.lt = new Node(6);
root.rt.rt = new Node(7);
BFS(root);
}
public static void BFS(Node root) {
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
int L = 0; //루트 노드는 0
while (!queue.isEmpty()){
int len = queue.size();
System.out.print(L + " : ");
for (int i = 0; i < len; i++) {
Node currentNode = queue.poll(); // 큐에서 하나 꺼내고 출력
System.out.print(currentNode.data + " ");
if(currentNode.lt!=null) queue.offer(currentNode.lt);
if(currentNode.rt!=null) queue.offer(currentNode.rt);
}
L++;
System.out.println();
}
}
}반응형
'알고리즘 문제풀이 입문: 코딩테스트 대비 > 섹션 7. Recursive, Tree, Graph(DFS,BFS 기초)' 카테고리의 다른 글
| 경로탐색 (인접 행렬 / 인접 리스트) (0) | 2024.05.09 |
|---|---|
| Tree 말단 노드까지 가장 짧은 경로 (DFS, BFS) (0) | 2024.05.08 |
| 부분집합 구하기 (DFS) (0) | 2024.04.30 |
| 이진트리 순회 (DFS : Depth-First Search) (0) | 2024.04.29 |
| 피보나치 재귀 (메모이제이션) (0) | 2024.04.29 |



