설명
N*N의 섬나라 아일랜드의 지도가 격자판의 정보로 주어집니다.
각 섬은 1로 표시되어 상하좌우와 대각선으로 연결되어 있으며, 0은 바다입니다.
섬나라 아일랜드에 몇 개의 섬이 있는지 구하는 프로그램을 작성하세요.
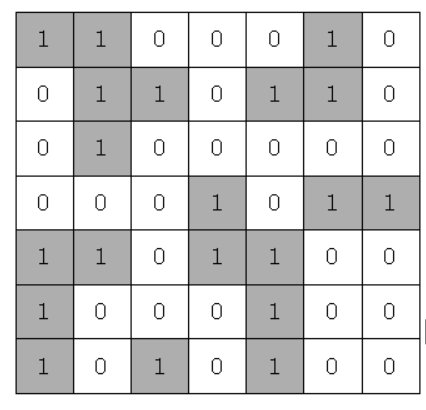
만약 위와 같다면 섬의 개수는 5개입니다.
입력
첫 번째 줄에 자연수 N(3<=N<=20)이 주어집니다.
두 번째 줄부터 격자판 정보가 주어진다.
출력
첫 번째 줄에 섬의 개수를 출력한다.
예시 입력 1
7
1 1 0 0 0 1 0
0 1 1 0 1 1 0
0 1 0 0 0 0 0
0 0 0 1 0 1 1
1 1 0 1 1 0 0
1 0 0 0 1 0 0
1 0 1 0 1 0 0
예시 출력 1
5
문제 해결
2차원 격자판에서 서로 연결된 섬들을 찾아 개수를 세는 문제이다.
같은 문제에 대해 DFS와 BFS 두 방식으로 문제를 풀어보았다.
static int N;
static int[][] map;
static boolean[][] visited;
static int[] dx = {-1, -1, -1, 0, 0, 1, 1, 1}; // x축 이동
static int[] dy = {-1, 0, 1, -1, 1, -1, 0, 1}; // y축 이동
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
N = in.nextInt();
map = new int[N][N];
visited = new boolean[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
map[i][j] = in.nextInt();
}
}
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (map[i][j] == 1 && !visited[i][j]) {
DFS(i, j);
count++;
}
}
}
System.out.println(count);
위 부분까지는 공통적인 코드로 작성했다.
- map은 2차원 격자판의 정보를, visited 배열은 특정 위치를 방문했는지의 여부를 기록 저장하고
- dx와 dy 배열은 대각선까지 포함해 총 8방향에 대한 이동방향을 나타낸다.
N x N 크기의 격자판 정보를 입력받고, 섬의 개수를 세어줄 count변수를 0으로 초기화해준 후 각각 행과 열을 돌며 격자판의 모든 곳을 방문하며, 현재 위치가 섬이고, 아직 방문하지 않았다면 DFS 혹은 BFS를 호출하는 코드이다.
새로운 섬을 발견했다면 count를 증가시키고, 최종적으로 발견된 모든 섬의 개수를 출력해준다.
< DFS >
DFS의 경우 하나의 경로를 끝까지 탐색하고 다시 돌아와 다른 경로를 탐색하는 재귀 호출로 구현된다.
public static void DFS(int x, int y) {
visited[x][y] = true;
for (int i = 0; i < 8; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < N && ny >= 0 && ny < N && map[nx][ny] == 1 && !visited[nx][ny]) {
DFS(nx, ny);
}
}
}- 현재 위치에서 상하좌우, 대각선으로 이동할 수 있으므로 8for문을 돌며 새로운 x좌표와 y좌표를 계산하고
- 새로운 좌표가 범위를 벗어나지 않았고, 섬이며 아직 방문하지 않았으면 DFS를 호출한다.
< BFS >
BFS의 경우 현재 노드라 인접한 노드들을 탐색하고 다음 레벨 (깊이)을 호출하는 식으로 구현된다.
static void BFS(int x, int y) {
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{x, y});
visited[x][y] = true;
while (!queue.isEmpty()) {
int[] current = queue.poll();
int cx = current[0];
int cy = current[1];
for (int i = 0; i < 8; i++) {
int nx = cx + dx[i];
int ny = cy + dy[i];
if (nx >= 0 && ny >= 0 && nx < N && ny < N && map[nx][ny] == 1 && !visited[nx][ny]) {
visited[nx][ny] = true;
queue.add(new int[]{nx, ny});
}
}
}
}- 큐에 x와 y 좌표를 저장해야하므로 int[] 배열을 저장한다. => ㄲ각 ,y좌표를 배열로 저장하고 시작 위치의 방문 여부를 true로 설정한다.
- 큐가 비어있는 동안
- 큐에 들어있는 요소 중 가장 위에 있는 것을 꺼내 current 배열에 저장하고, 각각의 x,y좌표를 cx, cy에 저장한다.
- 현재 위치에서 상하좌우, 대각선으로 이동할 수 있으므로 8for문을 돌며 새로운 x좌표와 y좌표를 계산하고, 새로운 좌표가 범위를 벗어나지 않았고, 섬이며 아직 방문하지 않았으면
- 새 좌표의 방문 여부를 true로 업데이트하고
- 새로운 위치를 큐에 추가하면 된다.
최종 코드
< DFS >
import java.util.Scanner;
public class P13_섬나라아일랜드_DFS {
static int N;
static int[][] map;
static boolean[][] visited;
static int[] dx = {-1, -1, -1, 0, 0, 1, 1, 1}; // x축 이동
static int[] dy = {-1, 0, 1, -1, 1, -1, 0, 1}; // y축 이동
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
N = in.nextInt();
map = new int[N][N];
visited = new boolean[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
map[i][j] = in.nextInt();
}
}
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (map[i][j] == 1 && !visited[i][j]) {
DFS(i, j);
count++;
}
}
}
System.out.println(count);
}
public static void DFS(int x, int y) {
visited[x][y] = true;
for (int i = 0; i < 8; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < N && ny >= 0 && ny < N && map[nx][ny] == 1 && !visited[nx][ny]) {
DFS(nx, ny);
}
}
}
}
< BFS >
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class P14_섬나라아일랜드_BFS {
static int N;
static int[][] map;
static boolean[][] visited;
static int[] dx = {-1, -1, -1, 0, 0, 1, 1, 1}; // x축 이동
static int[] dy = {-1, 0, 1, -1, 1, -1, 0, 1}; // y축 이동
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
N = in.nextInt();
map = new int[N][N];
visited = new boolean[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
map[i][j] = in.nextInt();
}
}
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (map[i][j] == 1 && !visited[i][j]) {
BFS(i, j);
count++;
}
}
}
System.out.println(count);
}
static void BFS(int x, int y) {
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{x, y});
visited[x][y] = true;
while (!queue.isEmpty()) {
int[] current = queue.poll();
int cx = current[0];
int cy = current[1];
for (int i = 0; i < 8; i++) {
int nx = cx + dx[i];
int ny = cy + dy[i];
if (nx >= 0 && ny >= 0 && nx < N && ny < N && map[nx][ny] == 1 && !visited[nx][ny]) {
visited[nx][ny] = true;
queue.add(new int[]{nx, ny});
}
}
}
}
}
반응형
'알고리즘 문제풀이 입문: 코딩테스트 대비 > 섹션 8. DFS, BFS 활용' 카테고리의 다른 글
| 피자 배달 거리(삼성 SW역량평가 기출문제 : DFS활용) (0) | 2024.05.20 |
|---|---|
| 토마토(BFS 활용) (0) | 2024.05.18 |
| 미로의 최단거리 통로(BFS) (0) | 2024.05.18 |
| 미로 탐색 (DFS) (0) | 2024.05.15 |
| 조합 구하기 (0) | 2024.05.15 |



